qertrocks.blogg.se

• Converting recurring decimals to fractions how to#

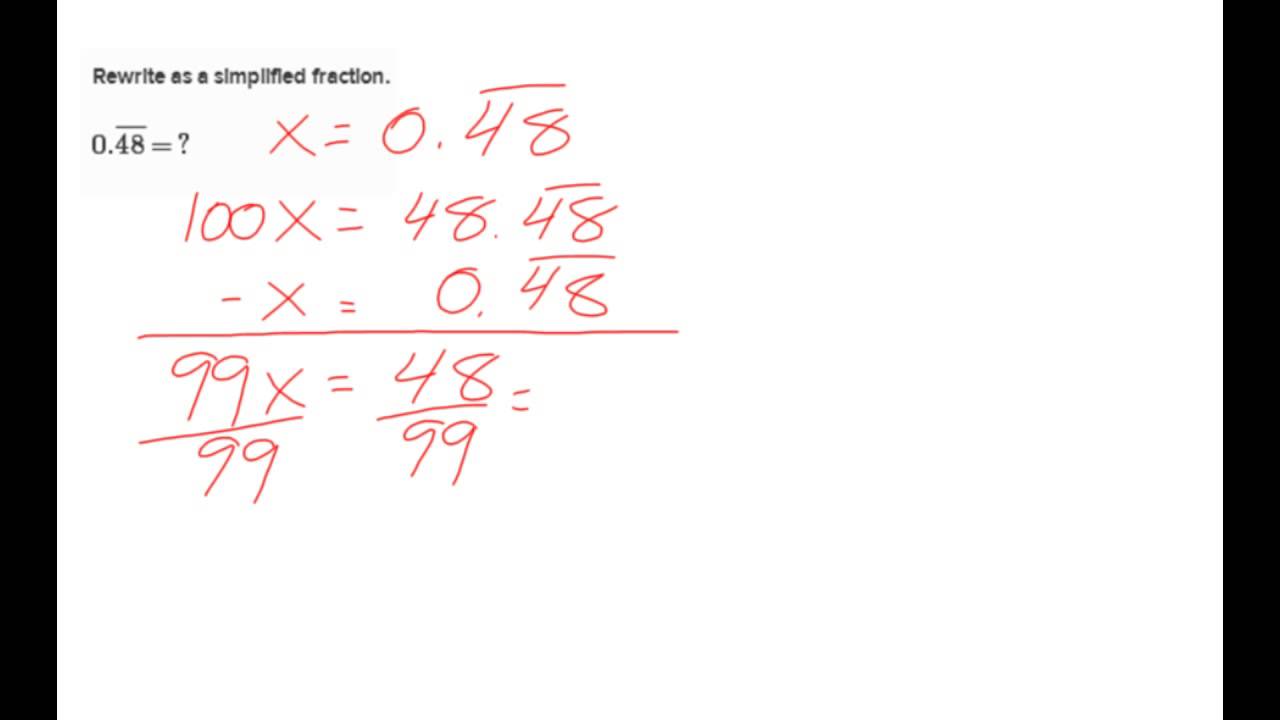
The smallest power of 10 that will work is 100: 1 0 0 𝑁 = 3 4. Results are a number with the same repeating decimal starting straight after the decimal We will have to multiply 𝑁 by two different powers of 10, so that both That the repeating decimal does not start straight after the decimal point. Repeating part: it is the digit with the bar on the top, “7.” And we notice 𝑁 as a fraction in its simplest form, we need first to identify the

Let us look at two more complex examples to deepen our understanding of the method.Įxample 5: Converting a Repeating Decimal to a Fraction ̇ 3, which can be simplified toįrom this, by dividing both sides of the equation by 9, the value of 𝑁 can 𝑁 by 10, we find another number with exactly the same repeating decimal:ġ 0 𝑁, we find 1 0 𝑁 − 𝑁 = 3. For the sake ofĬlarity, we are going to call this number 𝑁. Repeating after the decimal point leads to an integer. Realization that subtracting two repeating decimals that have exactly the same decimal part ̇ 3, that it canīe written as 1 3? We are going to learn a simple method based on the The bar notation is often used to indicate that a digit or group of digits is A repeating decimal occurs when the division To convert repeating decimals to a fraction. So far, we have looked at examples with terminating decimals. There is no common factor between 27 andĥ0 except 1 therefore, this fraction is in its simplest form. Multiples of 2, we can divide both the numerator and denominator by 2:ĥ 4 1 0 0 = 2 7 5 0. Then, we express this improper fraction as a mixed number:įinally, we find the simplest form of the fractional part. We are asked to write 4.54 as a mixed number in its simplest form.įirst, we convert 4.54 into a fraction: 4. The age of Earth is given here as a number of billion years, and it is given as aĭecimal, 4.54. The age of Earth is about 4.54 billion years. We are going to look at some examples to check our understanding.Įxample 3: Converting a Decimal to a Mixed Number This fraction is a so-called improper fraction since its numerator is greater than itsĭenominator. Simplified any further since 343 is a multiple of neither 5 nor 2, which are the only two We can do this in our example by simplifying by two twice:ġ 3 7 2 1 0 0 0 = 6 8 6 5 0 0 = 3 4 3 2 5 0.

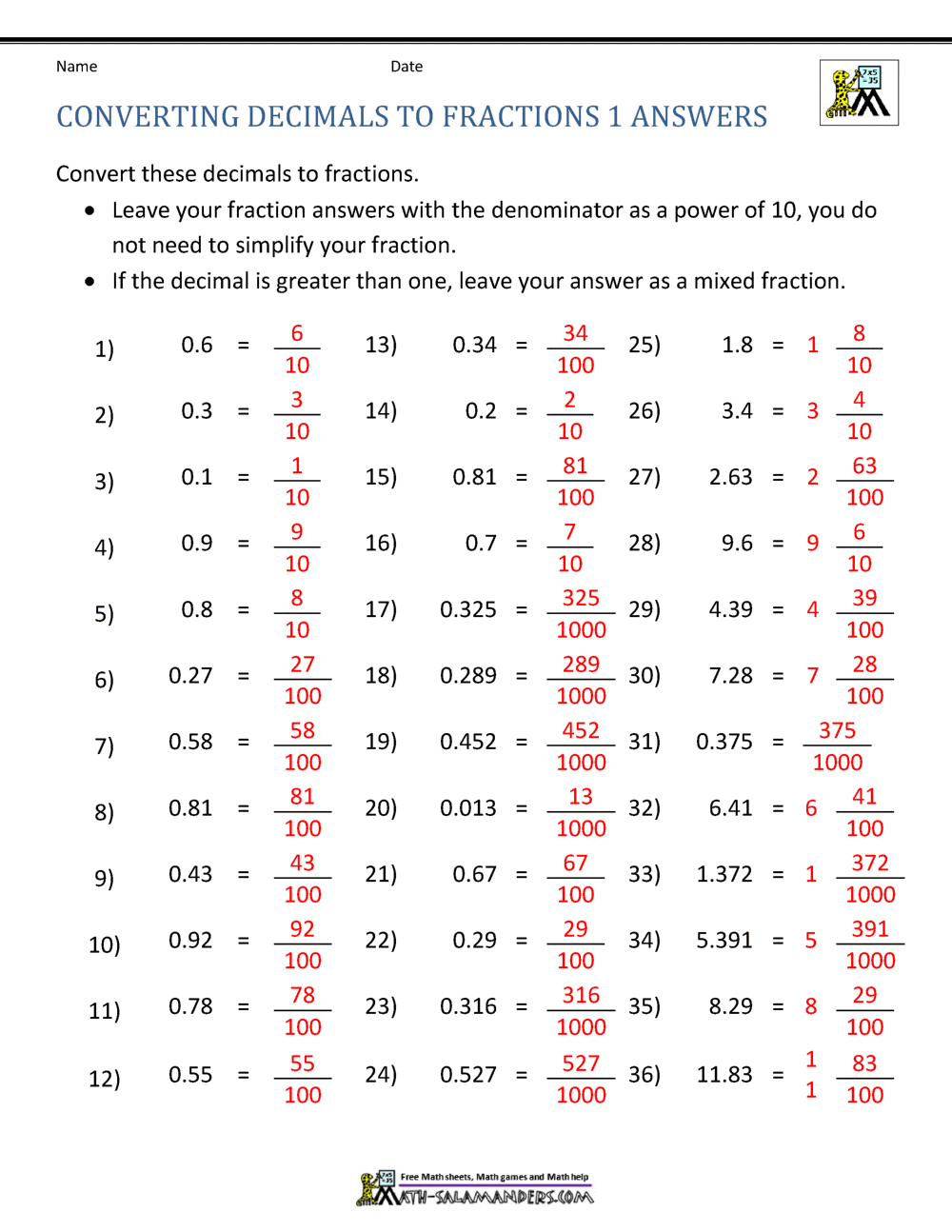
Now, we may want to express this fraction So far, we have converted a decimal to a fraction. To find the denominator, we can simply multiply our number by the value of the denominator:ġ. That it is in the thousandths column, so the simplest denominator to start with is 1‎ ‎000. A last digit in the third position after the decimal point means We see that, in this method, the position of the last digit of a number determines theĭenominator of the fraction.

Converting recurring decimals to fractions how to#

We are going to learn here how to convert a decimal back to a fraction 7 5, a rational number can beĮxpressed as a decimal. A rational number is a real number that can be expressed as a simple fraction (i.e., whoseĪs we have seen above with 3 4 = 0.